An evaluation of GPU filters for accelerating the 2D convex hull

Abstract

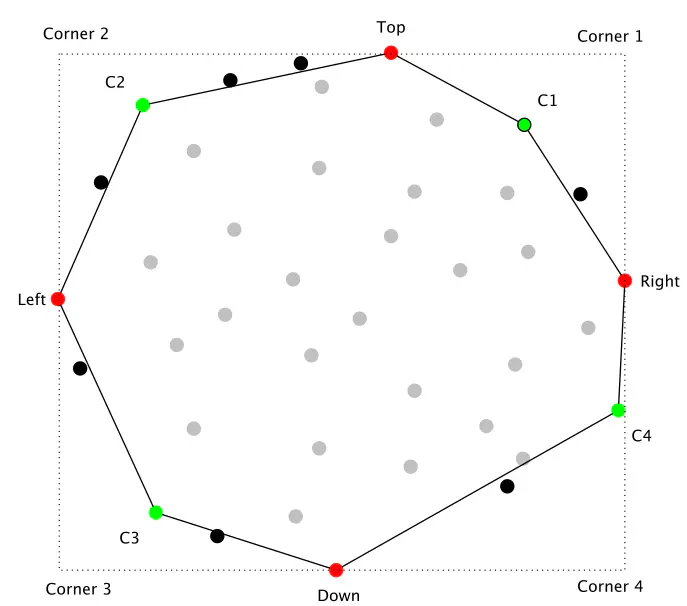
The Convex Hull is one of the most relevant structures in computational geometry, with many applications such as in computer graphics, robotics, and data mining. Despite the advances in the new algorithms in this area, it is often needed to improve the performance to solve more significant problems quickly or in real-time processing. This work presents an experimental evaluation of GPU filters to reduce the cost of computing the 2D convex hull. The techniques first perform a preprocessing of the input set, filtering all points within an eight-vertex polygon to obtain a reduced set of candidate points. We use parallel computation and the use of the Manhattan distance as a metric to find the vertices of the polygon and perform the point filtering. For the filtering stage we study different approaches; from custom CUDA kernels to libraries such as Thrust and Cub. Four types of point distributions are tested: a normal distribution (favorable case), uniform (favorable case), circumference (the worst case), and a case where points are shifted randomly from the circumference (intermediate case). The experimental evaluation shows that the GPU filtering algorithm can be up to 17.5× faster than a sequential CPU implementation, and the whole convex hull computation can be up to 160× faster than the fastest implementation provided by the CGAL library for a uniform distribution and 23× for a normal distribution.